激活函数 - Echo's Blog

激活函数的相关知识。常用的激活函数公式和函数图像。

为什么神经网络需要激活函数？

当我们不用激活函数时，权重和偏差只会进行线性变换。线性方程很简单，但解决复杂问题的能力有限。

没有激活函数的神经网络实质上只是一个线性回归模型。激活函数对输入进行非线性变换，使其能够学习和执行更复杂的任务。我们希望我们的神经网络能够处理复杂任务，如语言翻译和图像分类等。线性变换永远无法执行这样的任务。

激活函数使反向传播成为可能，因为激活函数的误差梯度可以用来调整权重和偏差。如果没有可微的非线性函数，这就不可能实现。总之，激活函数的作用是能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。

为什么激活函数需要非线性函数？

假若网络中全部是线性部件，那么线性的组合还是线性，与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数。
使用非线性激活函数，以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性激活函数，能够从输入输出之间生成非线性映射。

改善激活函数的原因？

神经网络发展缓慢的一个因素就是激活函数最原始的时候采用了sigmoid函数，在传播过程中极易出现梯度爆炸和梯度消失的问题，这一点也是网络层数受到限制的原因。后来的ReLU可以说优化了这一点，但并没有完全解决。

缓解梯度问题
引入非线性特征
抑制神经元死亡
稀疏激活
兼容性
减少计算开销

激活函数有哪些性质？

非线性：当激活函数是非线性的，一个两层的神经网络就可以基本上逼近所有的函数。但如果激活函数是恒等激活函数的时候，即 $ f(x)=x $，就不满足这个性质，而且如果 MLP 使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的；
可微性：当优化方法是基于梯度的时候，就体现了该性质；
单调性：当激活函数是单调的时候，单层网络能够保证是凸函数；
$ f(x)≈x $：当激活函数满足这个性质的时候，如果参数的初始化是随机的较小值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要详细地去设置初始值；
输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况下，一般需要更小的 Learning Rate。

常用激活函数

step

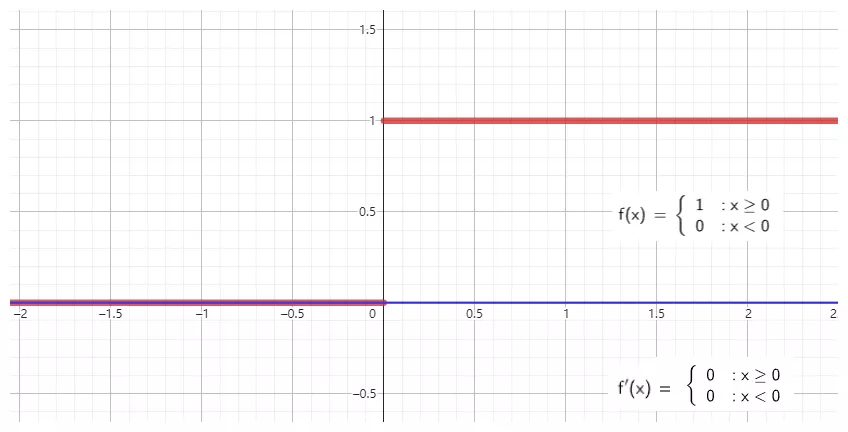
step 有时也被称作 Binary Step 或者 Heaviside，它的理论价值远超过其应用价值，step 能完美诠释神经元的激活含义：当刺激超过阈值的时候才会激发。但是由于它的梯度始终为 0，所以并不能用作神经网络的激活函数。详细信息请看下图：

Sigmoid

$$ f(x) = \frac{1}{1 + e^{-x}} $$

其值域为 $ (0,1) $。

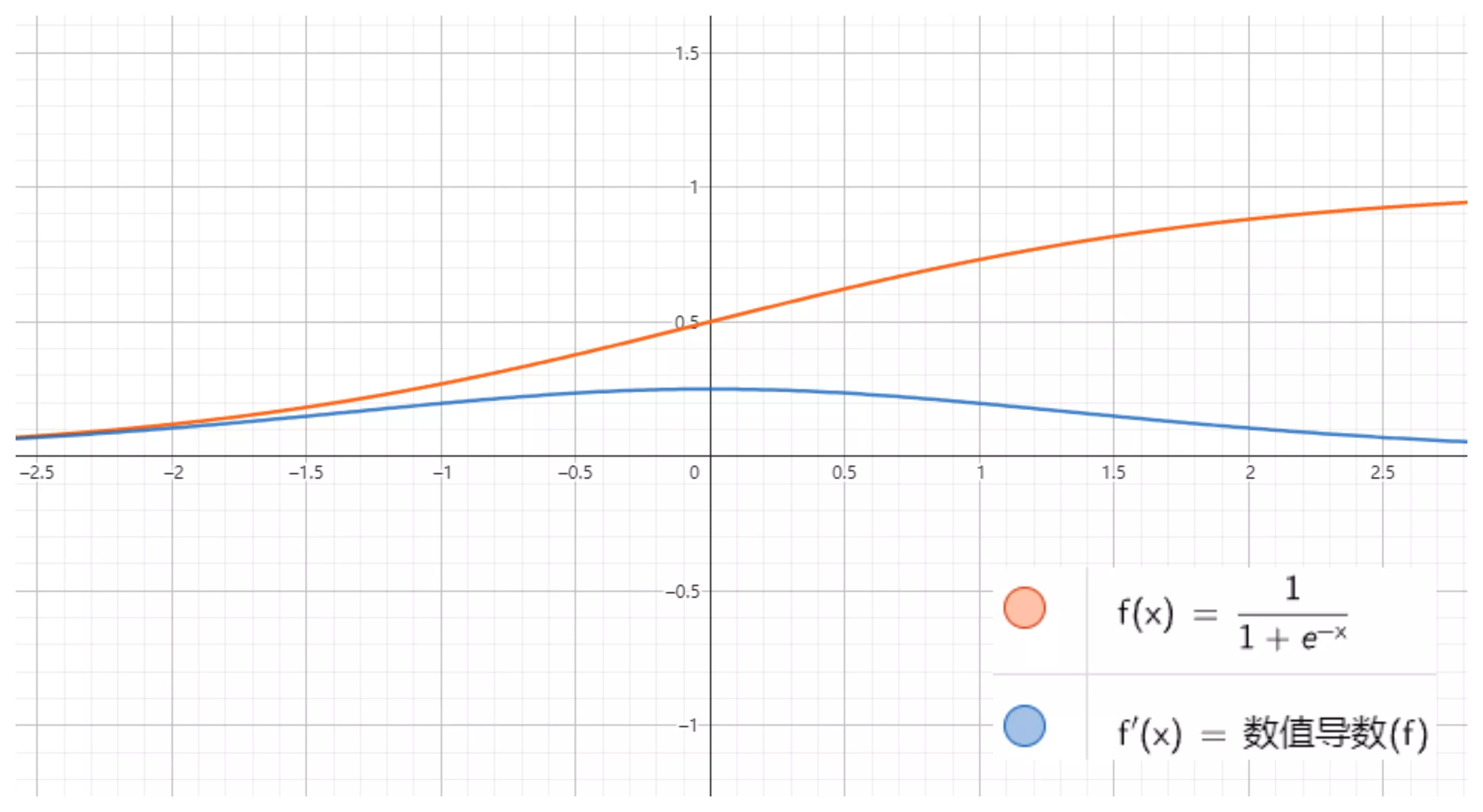
sigmoid 是使用范围最广的一类激活函数，具有指数函数形状，它在物理意义上最为接近生物神经元。此外，(0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如 Sigmoid 交叉熵损失函数。

然而，sigmoid 也有其自身的缺陷，最明显的就是饱和性。从下图可以看到，其两侧导数逐渐趋近于 0 。具有这种性质的称为软饱和激活函数。具体的，饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和。

优点：

输出范围在0到1之间，适合用于二元分类问题。
具有平滑的梯度，容易训练。

缺点：

Sigmoid函数在输入值较大或较小的情况下，梯度接近于零，导致梯度消失问题。这会导致梯度下降变得缓慢，难以训练深层网络。
输出不是零中心化（因为靠近0时，值为0.5），可能导致梯度更新不均匀，使得某些权重更新过于激烈。
改进激活函数：ReLU、Leaky ReLU、Parametric ReLU (PReLU)等。

sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid 向下传导的梯度包含了一个 f′(x) 因子（sigmoid 关于输入的导数），因此一旦输入落入饱和区，f′(x) 就会变得接近于 0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。

Tanh

函数的定义为：

$$ f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} $$

值域为 $ (-1,1) $。$ f'(x) = 1 - f^2(x) $

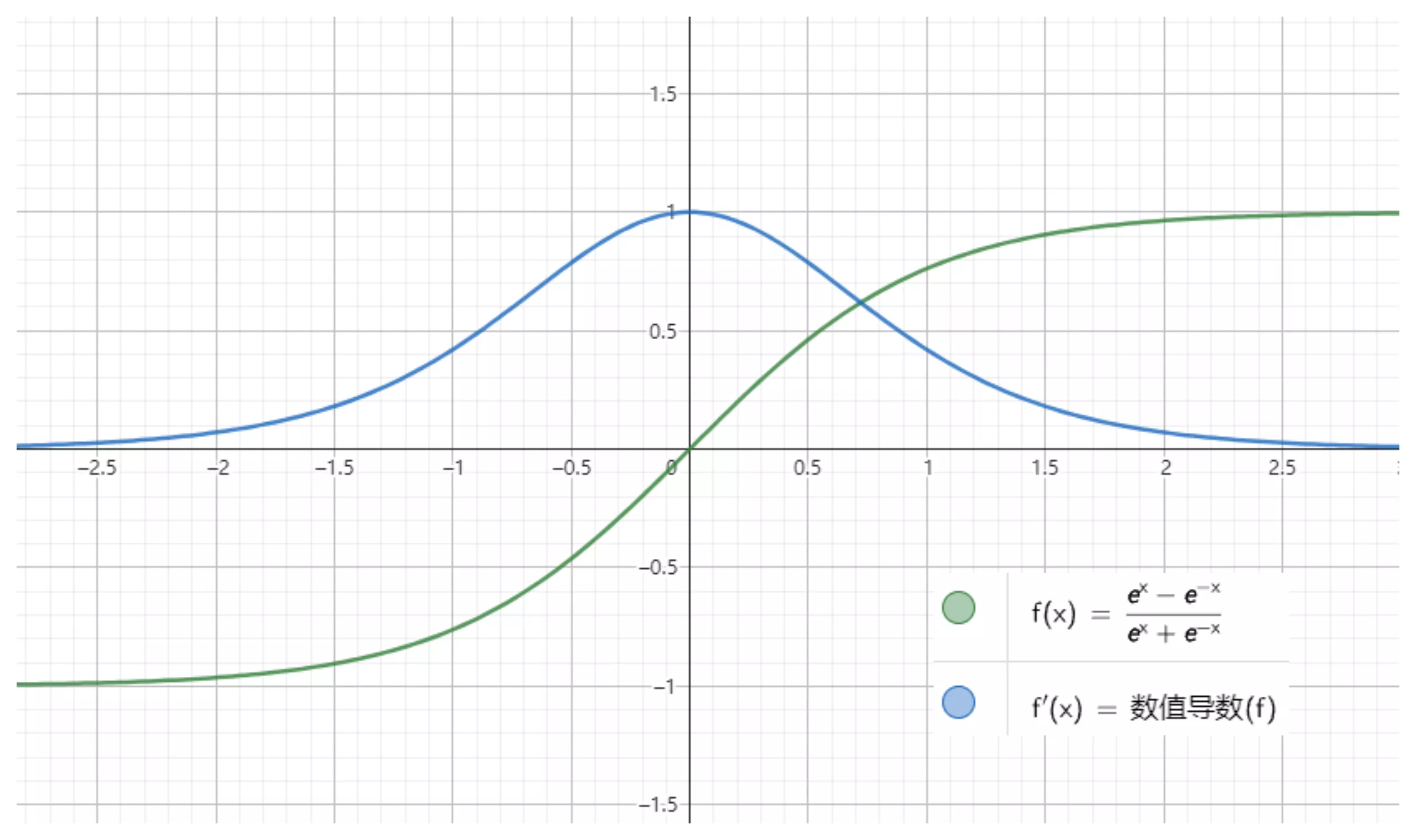
tanh 是双曲正切函数，tanh 函数和 sigmod 函数的曲线是比较相近的，咱们来比较一下看看。首先相同的是，这两个函数在输入很大或是很小的时候，输出都几乎平滑，梯度很小，不利于权重更新；不同的是输出区间，tanh 的输出区间是在 (-1,1) 之间，而且整个函数是以 0 为中心的，这个特点比 sigmod 的好。

一般二分类问题中，隐藏层用 tanh 函数，输出层用 sigmod 函数。不过这些也都不是一成不变的，具体使用什么激活函数，还是要根据具体的问题来具体分析，还是要靠调试的。

优点：

输出范围在-1到1之间，零中心化，相对于Sigmoid有更好的性能。

缺点：

与Sigmoid一样，Tanh函数也存在梯度消失问题。
改进激活函数：ReLU、Leaky ReLU、PReLU等。

Identity

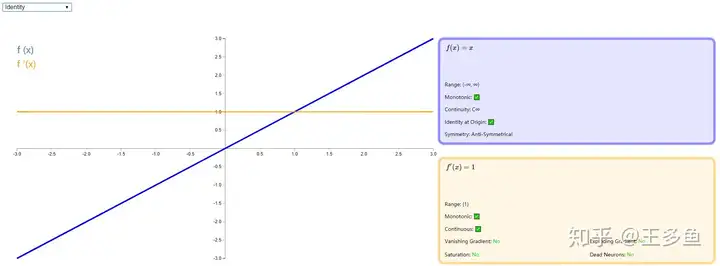
Identity 是一种输入和输出相等的激活函数，比较适合底层函数是线性的，比如线性回归问题，当存在非线性问题是，作用就大打折扣了。很少被用作隐藏层的激活函数，因为它不具备引入非线性特征的能力。

Identity激活函数在输出层某些情况下可能会用到，特别是在回归问题中，因为它可以输出任意实数值，适用于预测连续性的目标变量。例如，在线性回归中，输出层通常使用Identity激活函数。

数学表达式为：$ f(x) = x $

详细信息如下：

ReLU

函数的定义为：

$$ f(x) = max(0, x) $$

值域为 $ [0,+∞) $；

ReLU 全称是：Rectified linear unit, 是目前比较流行的激活函数，它保留了类似 step 那样的生物学神经元机制：输入超过阈值才会激发。虽然在 0 点不能求导，但是并不影响其在以梯度为主的反向传播中发挥有效作用。

优点：

相对于Sigmoid和Tanh，ReLU具有更好的计算性能，因为它是一个简单的线性函数。
只在正值范围内激活，有助于稀疏激活(只有少数神经元在给定输入下被激活，而大多数神经元的激活值保持不变或者接近于零)，减少模型的复杂性。

缺点：

ReLU存在一个问题称为“神经元死亡”问题，即在训练过程中，某些神经元可能永远不会被激活，导致无法更新它们的权重。
ReLU也容易引发梯度爆炸问题，尤其是在深层网络中。

改进激活函数：

Leaky ReLU：通过在负值范围内引入小的斜率来解决ReLU的神经元死亡问题。
Parametric ReLU (PReLU)：与Leaky ReLU类似，但允许斜率成为可学习参数。
Exponential Linear Unit (ELU)：在负值范围内具有平滑的曲线，缓解ReLU的问题，并具有零中心化的属性。

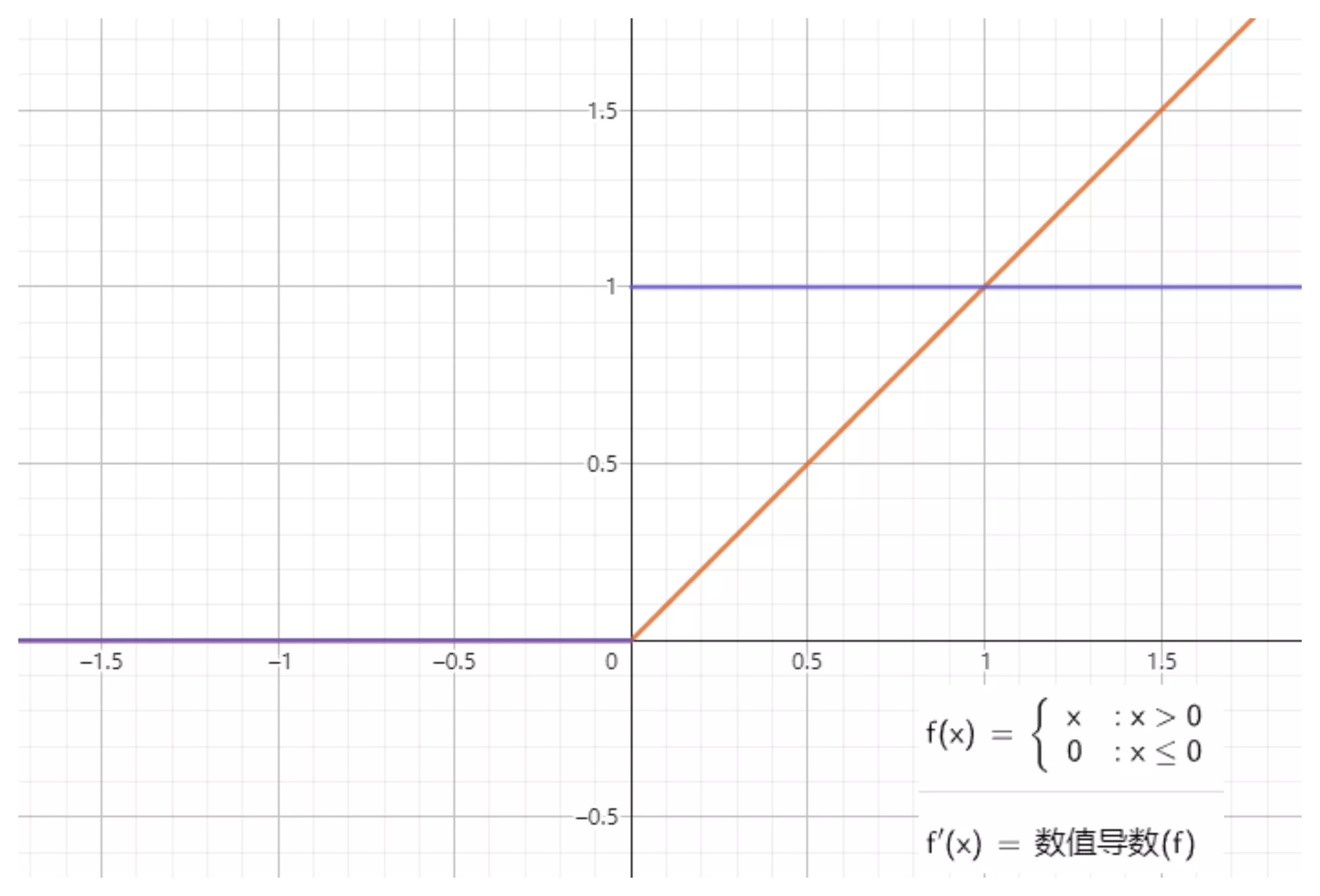
根据图像可看出具有如下特点：

单侧抑制；
相对宽阔的兴奋边界；
稀疏激活性；

ReLU 函数从图像上看，是一个分段线性函数，把所有的负值都变为 0，而正值不变，这样就成为单侧抑制。因为有了这单侧抑制，才使得神经网络中的神经元也具有了稀疏激活性。

稀疏激活性：从信号方面来看，即神经元同时只对输入信号的少部分选择性响应，大量信号被刻意的屏蔽了，这样可以提高学习的精度，更好更快地提取稀疏特征。当 $ x<0 $ 时，ReLU 硬饱和，而当 $ x>0 $ 时，则不存在饱和问题。ReLU 能够在 $ x>0 $ 时保持梯度不衰减，从而缓解梯度消失问题。

Leaky ReLU

值域为 $ (-∞,+∞) $。

由于 ReLU 在小于零的部分全部归为 0 ，这样极易造成神经元死亡，因此 Andrew L. Maas 等人在论文《Rectifier Nonlinearities Improve Neural Network Acoustic Models》中提出了新的激活函数，在小于 0 的方向增加一个非常小的斜率。如下图：

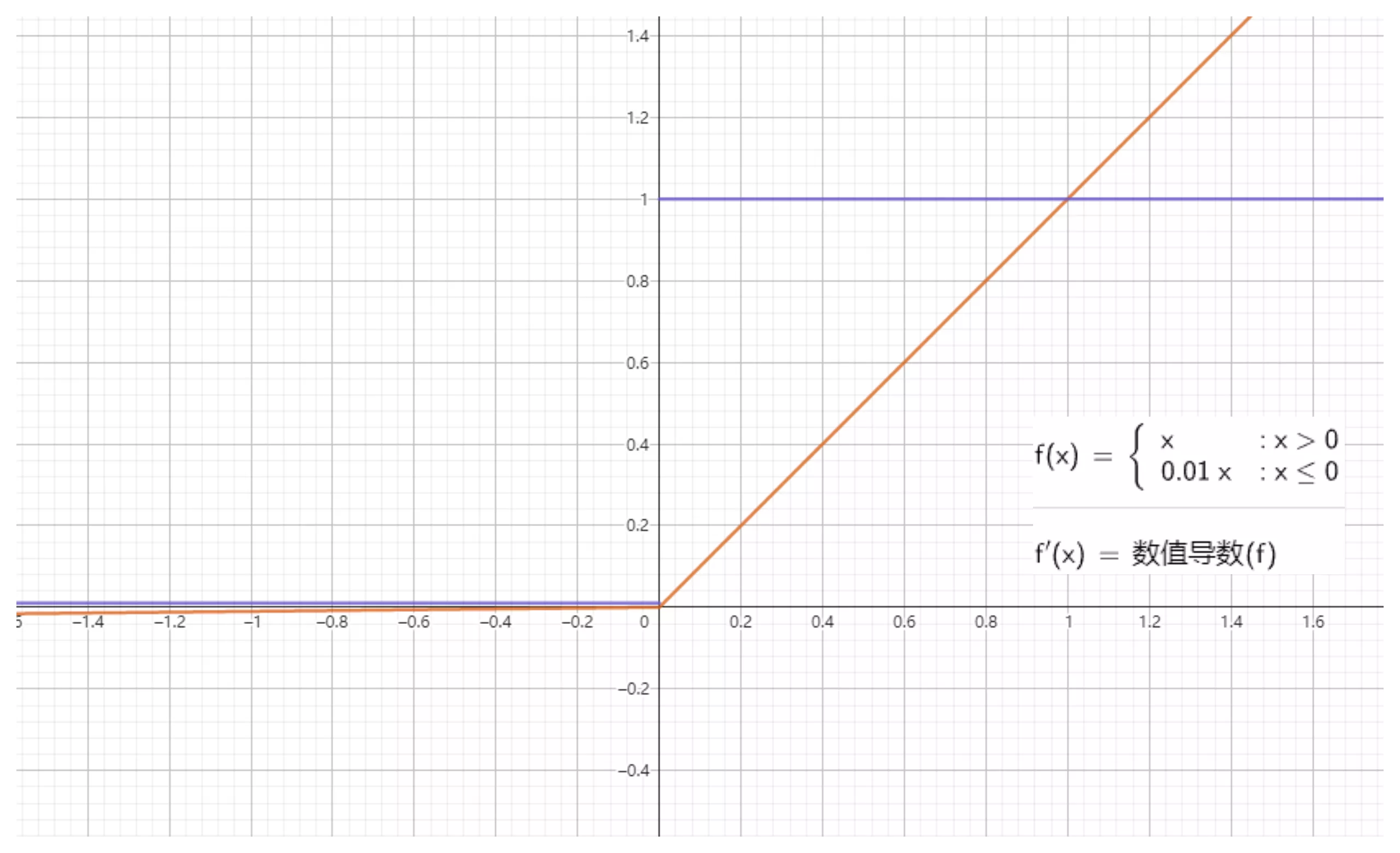
PReLU (Parameteric Rectified Linear Unit)

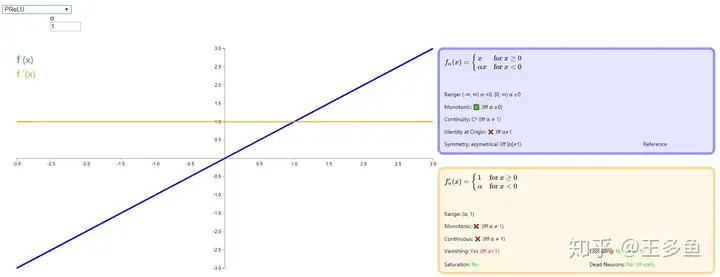
这个激活函数还是在优化 ReLU ，相比于 Leak ReLU，PReLU 将小于零的斜率换成了可变的参数 α。α 是一个可学习的参数，每个神经元都有一个对应的 α 值。在训练过程中，α 通过反向传播和梯度下降等优化算法来更新，以最小化损失函数。

当 α<0 时取值范围为 (−∞,∞)，当 α>=0 时取值范围为 [0,∞)。

详情可以参考原论文：《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》

softmax函数

Softmax 是一种形如下式的函数：

$$ P(i) = \frac{exp(\theta_i^T x)}{\sum_{k=1}^{K} exp(\theta_i^T x)} $$

其中，$ \theta_i $ 和 $ x $ 是列向量，$ \theta_i^T x $ 可能被换成函数关于 $ x $ 的函数 $ f_i(x) $。Softmax 多用于多分类神经网络输出。

通过 softmax 函数，可以使得 $ P(i) $ 的范围在 $ [0,1] $ 之间。在回归和分类问题中，通常 $ \theta $ 是待求参数，通过寻找使得 $ P(i) $ 最大的 $ \theta_i $ 作为最佳参数。

但是，使得范围在 $ [0,1] $ 之间的方法有很多，为啥要在前面加上以 $ e $ 的幂函数的形式呢？参考 logistic 函数： $ P(i) = \frac{1}{1+exp(-\theta_i^T x)} $ 这个函数的作用就是使得 $ P(i) $ 在负无穷到 0 的区间趋向于 0，在 0 到正无穷的区间趋向 1,。同样 softmax 函数加入了 $ e $ 的幂函数正是为了两极化：正样本的结果将趋近于 1，而负样本的结果趋近于 0。这样为多类别提供了方便（可以把 $ P(i) $ 看做是样本属于类别的概率）。可以说，Softmax 函数是 logistic 函数的一种泛化。

softmax 函数可以把它的输入，通常被称为 logits 或者 logit scores，处理成 0 到 1 之间，并且能够把输出归一化到和为 1。这意味着 softmax 函数与分类的概率分布等价。它是一个网络预测多分类问题的最佳输出激活函数。

如何选择激活函数？

选择一个适合的激活函数并不容易，需要考虑很多因素，通常的做法是，如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者测试集上进行评价。然后看哪一种表现的更好，就去使用它。

以下是常见的选择情况：

如果输出是 0、1 值（二分类问题），则输出层选择 sigmoid 函数，然后其它的所有单元都选择 ReLU 函数。
如果在隐藏层上不确定使用哪个激活函数，那么通常会使用 ReLU 激活函数。有时，也会使用 tanh 激活函数，但 ReLU 的一个优点是：当是负值的时候，导数等于 0。
sigmoid 激活函数：除了输出层是一个二分类问题基本不会用它。
tanh 激活函数：tanh 是非常优秀的，几乎适合所有场合。
ReLU 激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用 ReLU 或者 Leaky ReLU，再去尝试其他的激活函数。
如果遇到了一些死的神经元，我们可以使用 Leaky ReLU 函数。

使用 ReLU 激活函数的优点？

在区间变动很大的情况下，ReLU 激活函数的导数或者激活函数的斜率都会远大于 0，在程序实现就是一个 if-else 语句，而 sigmoid 函数需要进行浮点四则运算，在实践中，使用 ReLU 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快。
sigmoid 和 tanh 函数的导数在正负饱和区的梯度都会接近于 0，这会造成梯度弥散，而 Relu 和Leaky ReLu 函数大于 0 部分都为常数，不会产生梯度弥散现象。

需注意，Relu 进入负半区的时候，梯度为 0，神经元此时不会训练，产生所谓的稀疏性，而 Leaky ReLu 不会产生这个问题。

什么时候可以用线性激活函数？

回归问题的输出层，大多使用线性激活函数。其中目标是预测一个连续性的目标变量，例如房价、温度、销售额等。
在隐含层可能会使用一些线性激活函数。
一般用到的线性激活函数很少。